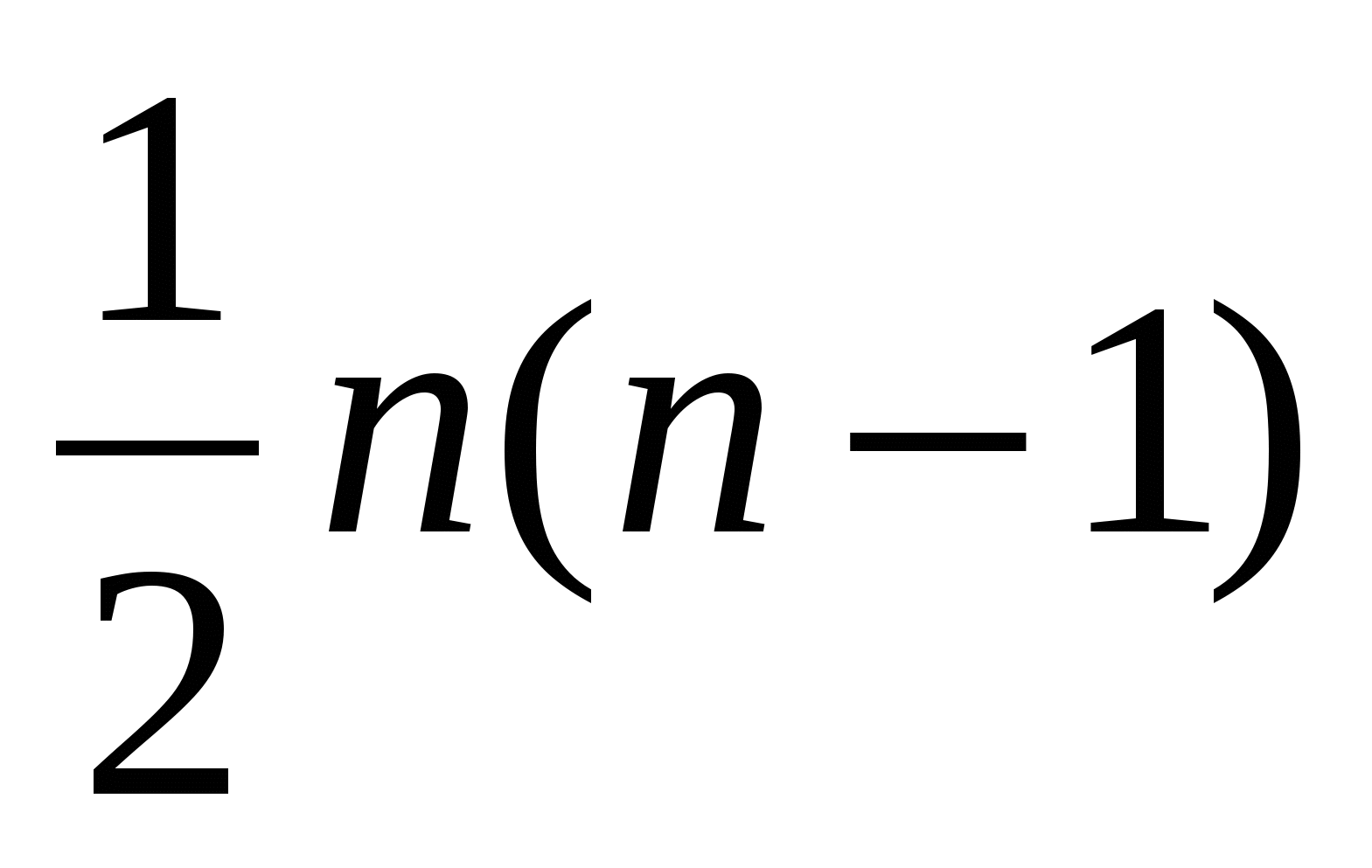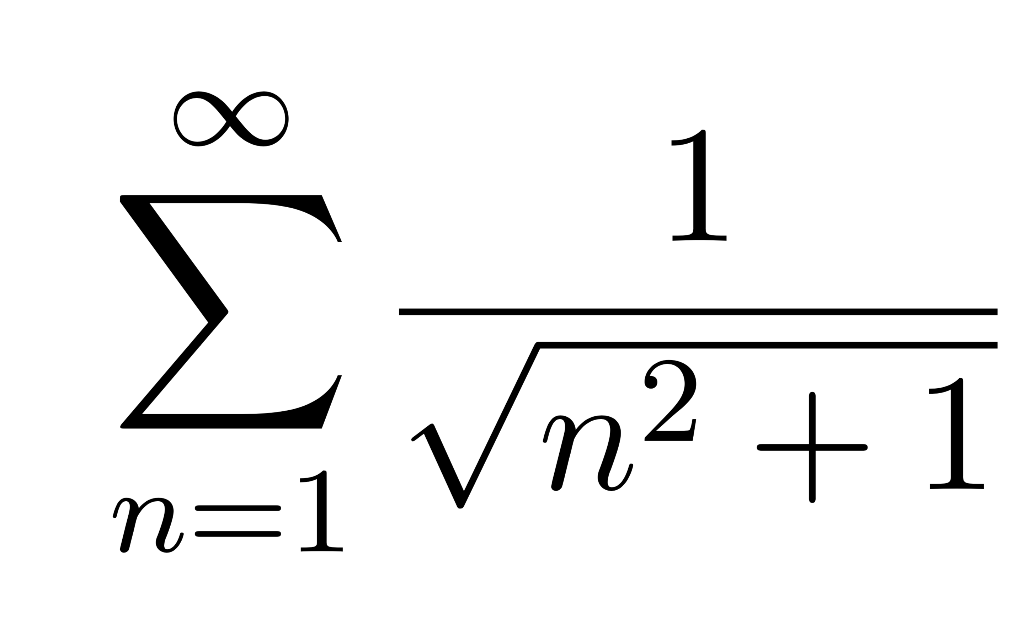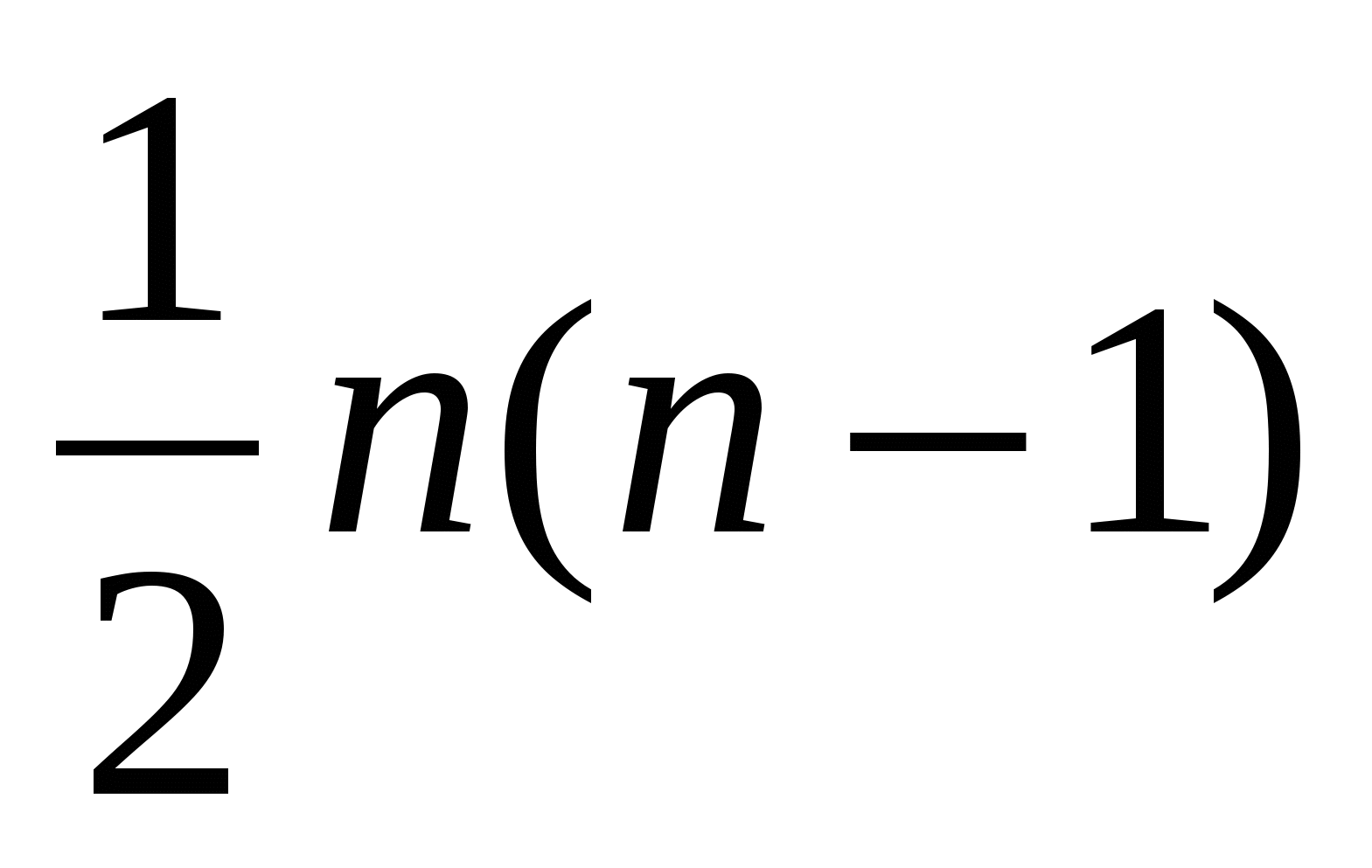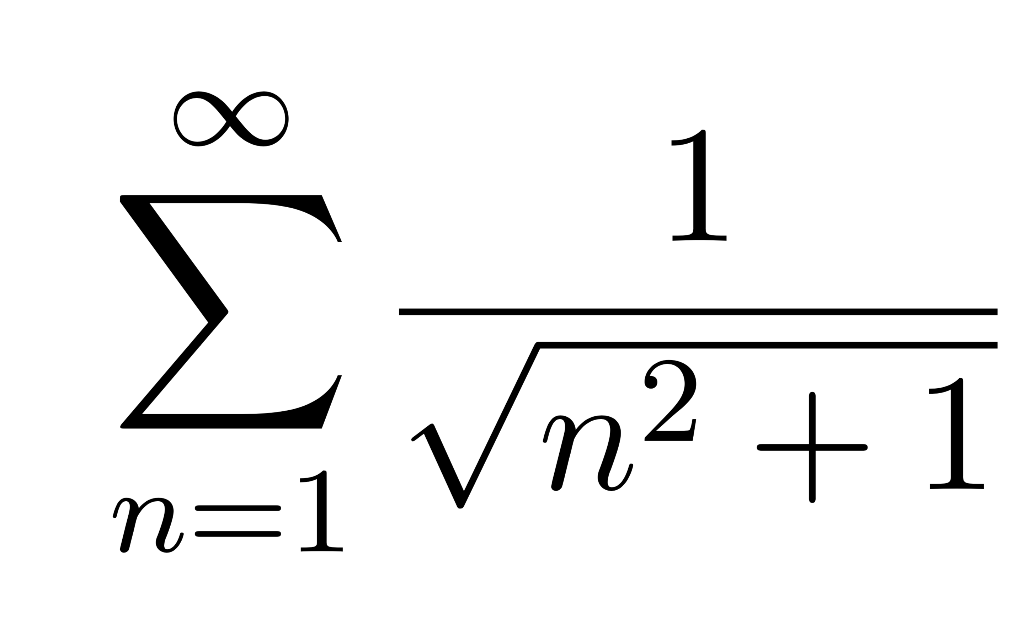N + (n-1) + (n-2)… + 1 = (n) (n + 1) / 2. 1 n 2 n ряд на сходимость. Упростите выражение (n+1)!/(n-2)!. 2n+1. Un формула.
|
Un 1 n 2 n. N + (-1)^n*2*n^2 - sqrt(n). ∑_(n=1)^∞(n/(2n+1) )^(n ) 〗. Сходимость ряда sin(1/n^2). (n - 1)! = решение.
|
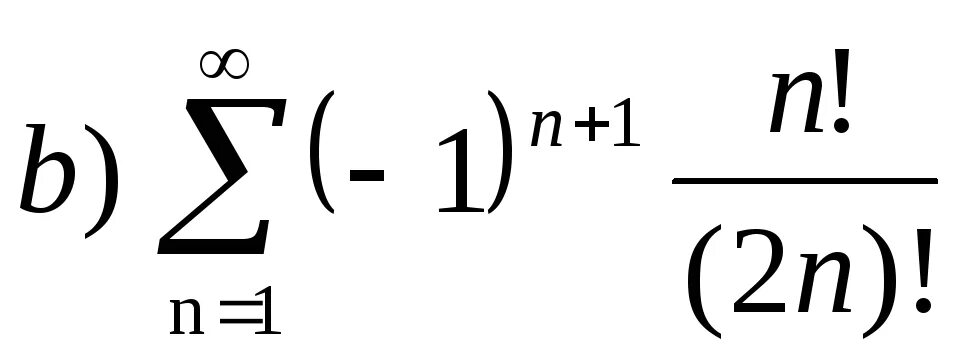Ряд sin 1/n. Un 1 n 2 n. (-1)^(n - 1)*(x-2)^2n/2n. An=1-2n/1+2n. A n+1 = 2a n - 3.
|
(1+1/n)^n. Сумма ряда 4/(n(n-1)(n-2)). (n+1)! - n!/(n+1)!. 1/(n+1) + 1/(n+2) +. Un 1 n 2 n.
|
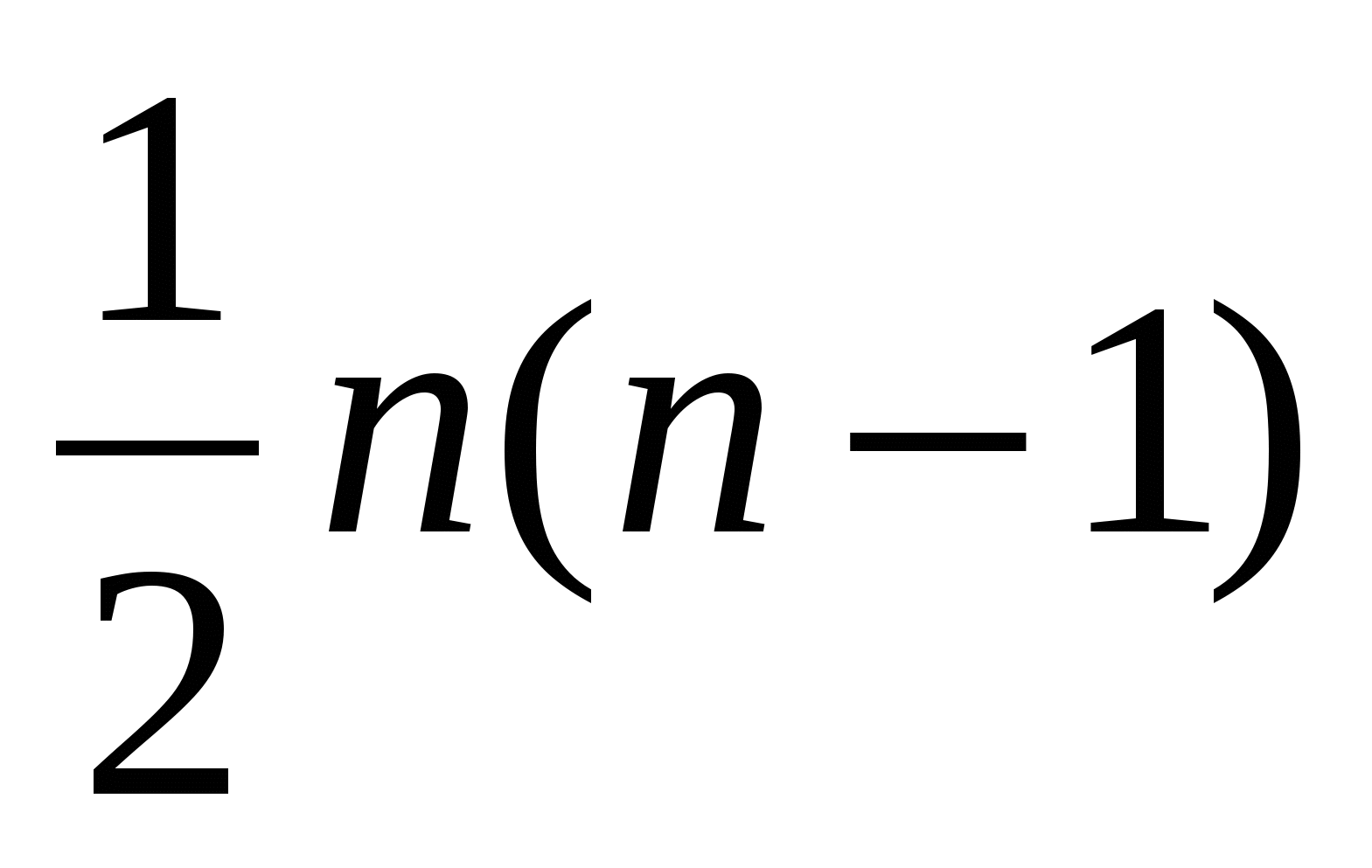Un 1 n 2 n. N(n-1)/2. Сумма ряда степеней. Название формулы u2/u1=n2/n1. Формула u1/u2 n1/n2.
|
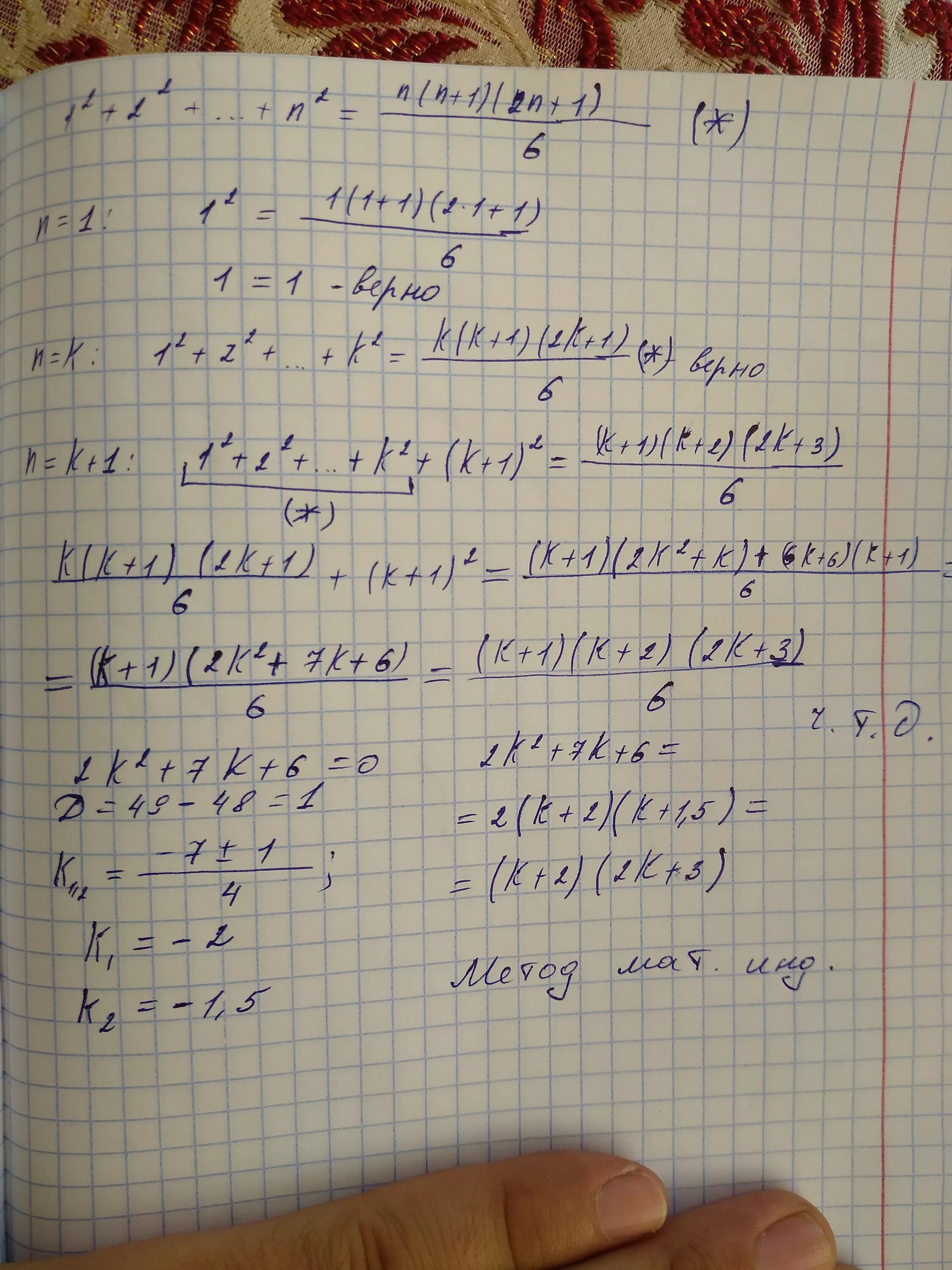Un 1 n 2 n. Сходимость ряда 2 + (-1)^n/2^n. Исследовать на сходимость ряд sin(1/n^2). + 1/(3n+1)>1. Пусть а 1 n+1.
|
Формула n*u. Предел 1/n+1. О((n+1)∗n/2)=о(n 2 ). -b(u-un) формула. Лимит (1/n^2 + 2/n^2 +.
|
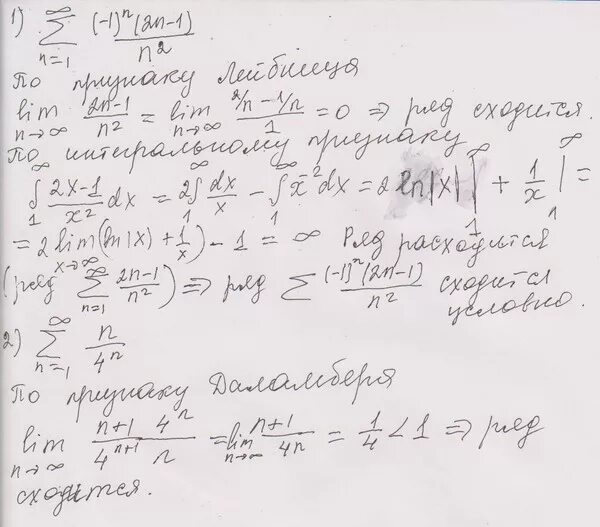Сумма ряда (2*3^n - 5^n)/15^n. Un 1 n 2 n. (1+1/n)^n. Sin 1/n сходимость ряда. Un 1 n 2 n.
|
1/n2-n+1/n2+n. U=m1u1+m2u2 формула u1. Упростить (n-1)!/(n+2)!. О((n+1)∗n/2)=о(n 2 ). Un 1 n 2 n.
|
Un 1 n 2 n. Un 1 n 2 n. Упростить n+1 n-1. Un 1 n 2 n. Un 1 n 2 n.
|
(2n-1)!<n^(2n-1). Сумма ряда 1/n(n+1)(n+2). (2n-1)/2^n. 〖(1+⋯+n)〗^2=〖((n(n+1))/2)〗^2. Исследовать ряды на сходимость n=3 n-2/(n-1)(n+1)n.
|
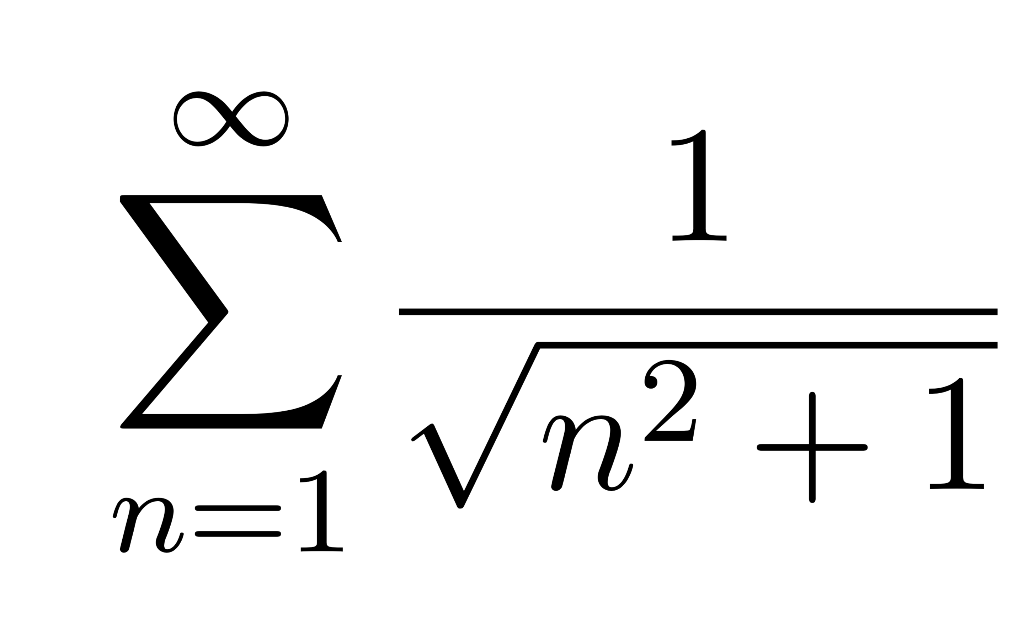Формула m и n в алгебре. (2n-1)!<n^(2n-1). Un 1 n 2 n. (1+1/n)^n. N^2+〖(n+1)〗^2+ …+〖(2n)〗^2.
|
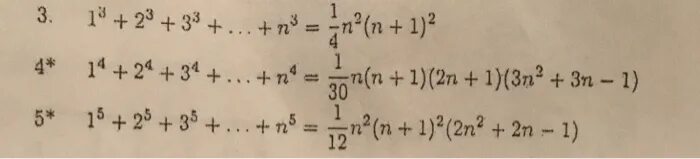Сходимость ряда x/(n^2+n*x). Un 1 n 2 n. Un 1 n 2 n. + (n-1/n^2)). (n+1)! - n!/(n+1)!.
|
Un 1 n 2 n. Sqrt(2)/2. Un 1 n 2 n. Un 1 n 2 n. Un 1 n 2 n.
|
Sqrt(n+2) -2sqrt(n+1) + sqrt(n). Un 1 n 2 n. (2n-1)/2^n. 1/n!-1/(n+1)!. Сходимость ряда sin(1/n^2).
|
(2n-1)!<n^(2n-1). N + (n-1) + (n-2)… + 1 = (n) (n + 1) / 2. (n+1)! - n!/(n+1)!. Исследовать на сходимость ряд sin(1/n^2). Сумма ряда 4/(n(n-1)(n-2)).
|
Un 1 n 2 n. Un 1 n 2 n. (2n-1)/2^n. Упростить (n-1)!/(n+2)!. (2n-1)!<n^(2n-1).
|
U=m1u1+m2u2 формула u1. Формула u1/u2 n1/n2. Sqrt(n+2) -2sqrt(n+1) + sqrt(n). Un 1 n 2 n. Сумма ряда (2*3^n - 5^n)/15^n.
|
Un 1 n 2 n. Un 1 n 2 n. Un 1 n 2 n. (n+1)! - n!/(n+1)!. Упростить (n-1)!/(n+2)!.
|
Un 1 n 2 n. Предел 1/n+1. A n+1 = 2a n - 3. Un 1 n 2 n. Un формула.
|